References
Introduction
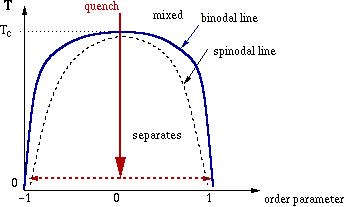
When an incompressible binary fluid mixture is quenched far below
its spinodal temperature, it will phase separate into domains of
the two fluids.
Here we study the simplest case - two fluids A and B have identical
properties in all respects except that they are mutually phobic - and
a deep quench so thermodynamic equilibrium has the two fluids completely
demixed.
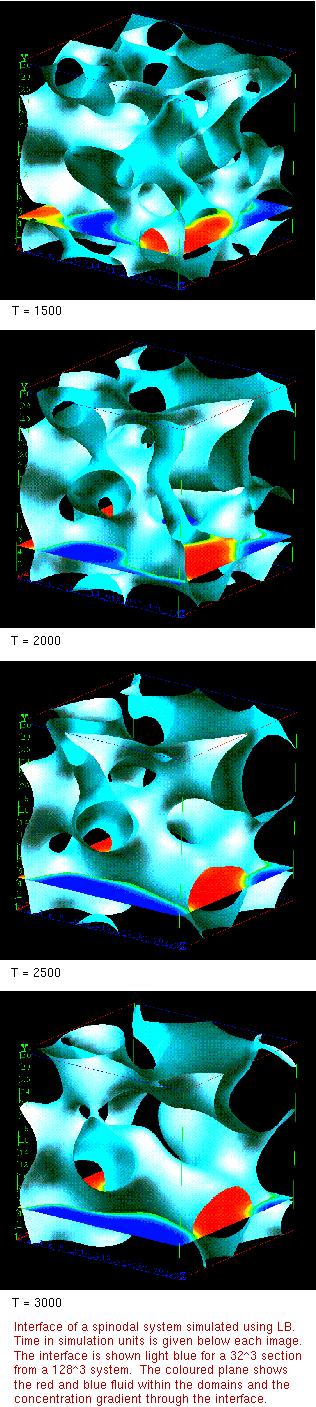
For a 50-50 mixture the two fluids form an interlocking structure as they
separate.
Shown in the diagram on the right is the interface between them at
successive times,
the interface is light blue, and the coloured plane shows the red/blue fluid
within the domains.
The late-stage growth is driven by capillary forces (Laplace pressure),
arising from curvature of the (sharply defined)
interface between the two fluids; these drive fluid flows from regions of
tight curvature (necks, narrow liquid bridges)
into those of low interfacial curvature (large domains).
Note that for coarsening of a bicontinuous structure to proceed this way,
one also requires
discrete ``pinch-off" events to continually occur: each of these allows
the topology to change discontinuously in time.
In the picture for time T=3000 (simulation units), a neck close to breaking point can be seen
towards the upper left of the image.
Besides the relative concentrations of the two fluids (50-50) and
the quench depth, the other significant parameters are the surface tension,
 ,
the viscosity,
,
the viscosity,
 ,
and the fluid mass density,
,
and the fluid mass density,
 ,
There is also a mobility parameter,
,
There is also a mobility parameter,
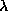 ,
which controls the diffusion.
,
which controls the diffusion.
More details of this work can be found in[Kendon et al.(1999)].
(Return to top.)
Model
This simple system is modeled by
a pair of coupled differential equations for the fluid velocity and
fluid composition. The fluid velocity obeys the Navier-Stokes equation with a
forcing term from the interface, which moves the fluid around as it
straightens and shrinks. The fluid composition is modeled as the difference
in density between the two fluids,
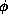 ,
which plays the role of the order parameter, and evolves via a
convection diffusion equation in which convection is provided by
the fluid velocity.
,
which plays the role of the order parameter, and evolves via a
convection diffusion equation in which convection is provided by
the fluid velocity.
The free energy, F, for the system is chosen to have
a double well potential with parameters determined so as to cause
sharp interfaces to form,
F =
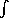 dr
dr
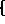 - A
- A
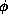 2
+ B
2
+ B
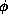 4
+ k(
4
+ k(

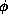 )2
+ 1/3
)2
+ 1/3
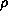 ln
ln
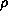
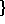 .
.
Parameters A and B control the shape and
depth of the double well, while k determines
the interfacial tension between the two fluids.
The interface width is about 6
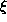 ,
where
,
where
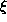 2
= k/2A.
2
= k/2A.
(Return to top.)
Theory
Given the above model, theory says that there should be three distinct,
universal growth regions[Bray(1994)]
for the average domain size, L:
- diffusive: L
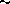 T1/3
for
T1/3
for
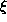
 L
L
 (
(
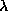
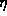 )1/2
(
)1/2
(
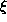 = molecular scale)
= molecular scale)
- viscous hydrodynamic: L
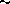 T
for
(
T
for
(
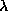
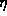 )1/2
)1/2
 L
L

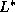
- inertial: L
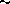 T2/3
for
L
T2/3
for
L
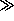
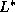
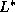 is a crossover length between the viscous hydrodynamic region,
where viscous drag is the main resistance to the driving force,
to the inertial region where finite Reynold's number effects come into play.
Theory predicts that
is a crossover length between the viscous hydrodynamic region,
where viscous drag is the main resistance to the driving force,
to the inertial region where finite Reynold's number effects come into play.
Theory predicts that
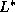 =
=
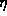 2 /
2 /
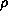
 ,
,
where  is the surface tension.
is the surface tension.
A prediction of a further crossover to a scaling in which
L scales as T1/2
was made recently
[Grant and Elder(1999)]. The argument is that
turbulence will develop as the system coarsens further into the
inertial region, and this will eventually remix the fluids by
disrupting the interface, slowing down the growth still further
from T2/3.
(Return to top.)
Comparison between different data sets
In order to compare different simulations
in a meaningful, universal way, we need to use length and time scales
based on the physical parameters of the system. For given values of
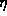 ,
,
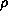 and
and
 ,
it is possible to form a characteristic length,
,
it is possible to form a characteristic length,
L0 =
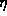 2 /
2 /
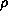
 ,
,
and a characteristic time,
T0 =
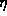 3 /
3 /
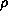
 2.
2.
Using L0 and T0
as the units of length and time, the scaling equations become,
L = b T -- linear region,
and,
L = c T2/3 -- inertial region,
where b and c are universal constants.
A useful non-dimensional measure used to characterise fluid systems is
the Reynolds number, Re,
defined as (velocity x length)/(kinematic viscosity).
For this system, the obvious choices of typical length and velocity are
L and dL/dT, giving
Re = L dL/dT, since in these
scaled units, with fluid density,
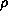 = 1,
the viscosity is equal to 1.
The Reynolds number gives an estimate of the ratio of the nonlinear term
in the Navier-Stokes equation, (v.
= 1,
the viscosity is equal to 1.
The Reynolds number gives an estimate of the ratio of the nonlinear term
in the Navier-Stokes equation, (v.  )v, to the viscous
term,
)v, to the viscous
term,
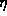
 2v, where v is the fluid velocity.
2v, where v is the fluid velocity.
(Return to top.)
Simulation and analysis methods
The above model equations have been simulated using a Lattice Boltzmann
(LB) method, on a D3Q15 lattice (see diagram, right). For details of the
method, see[Swift et al.(1996)]; details of the
code will appear in[Bladon and Desplat].
The simulations were run on the two of the parallel computers at the
Edinburgh Parallel Computing Centre,
a Cray T3D and a Hitachi SR-2201. The largest system size was
2563, using 256 processors on the T3D, and producing around
4Gb of output data in the form of order parameter and velocity fields
coarse-grained down to 1283.
The LB method allows the values of the viscosity, surface tension, fluid
density, interface width and mobility (diffusion) to be set; careful choice
of these parameters is necessary to ensure that the simulation
- remains stable through late times,
- maintains the interface profile in local equilibrium,
- limits the direct contribution from diffusion to the domain growth
to negligible values in the region of interest.
The order parameter data was analysed to extract a length scale using
Fourier transforms to obtain the first moment of the spherically averaged
structure factor.
The velocity field was also analysed using Fourier transforms to compute
derivatives, in order to compare the magnitude of the viscous and inertial
terms in the Navier-Stokes equation, and measure the skewness of the
longitudinal velocity derivatives.
(Return to top.)
Results
For each simulation run, the measured lengths (obtained from the order parameter data) and times have been
scaled using L0 and
T0
to form a single universal graph of
domain growth. (Also, in order to focus on the viscous and inertial regions,
any offset due to an initial diffusive period has been subtracted.)
This enabled all of
the main data runs to be displayed on a single log-log plot, see below,
covering five decades of reduced length and seven decades of reduced time.
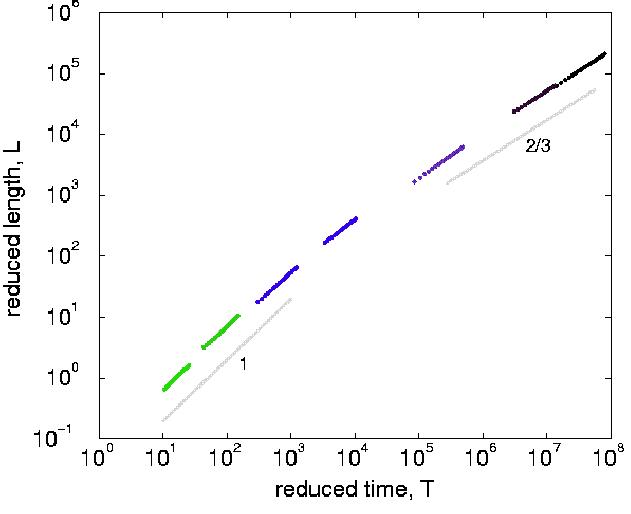
The eight main LB runs cover a linear region
1 < T < 102,
a long crossover region, 102 < T < 106 and
an inertial region 106 < T < 108,
so the predicted scaling behaviour is observed in our results.
No single run could cover the range of length and time scales presented
here, for that a simulation grid of around a million cubed would be required,
run for around 1010 time steps.
This is the first time the inertial region has been clearly observed
in simulation, see[Kendon et al.(1999)]
for discussion of other related work.
(Return to top.)
Inertial region
Since there are many factors that could produce a scaling that appears
to be T2/3,
we made a number of checks to make sure that our
observed results really are due to the simulation being in the inertial
region, and further, to see if the inertial nature of the fluid was leading
to the development of turbulence:
- we calculated the growth rate due to diffusion and then ensured that
data was only used for the final graph (above) if the diffusive
growth was under 2% of the total growth rate.
- to avoid finite size effects due to the periodic boundary conditions
causing the system to "interact with itself", an upper cut-off for the
data used was set at one quarter of the system size.
- from the velocity field, the individual terms in the Navier-Stokes
Equation were calculated, and the ratio of inertial to viscous terms
compared for each run, showing that in the linear region the viscous
term dominated over the inertial terms, and in the inertial region the
reverse was true.
- the skewness of the longitudinal velocity derivatives was calculated
- in turbulence this assumes a value of -0.5, in our most inertial run,
a value of -0.35 was found, which is consistent with patches of
turbulence developing within the domains, but not throughout the whole
system. Visualisation of the interface shows that it is not disrupted
by turbulent mixing, as might be the case if turbulence developed
throughout the system.
(Return to top.)
Conclusions
We have used a Lattice-Boltzmann method to
successfully simulate spinodal decomposition of a symetric, binary
fluid mixture in the linear (viscous hydrodynamic) region,
through a broad crossover to the inertial region where the domain size
scales as T2/3,
the first time the inertial region has been
unambiguously observed in simulation.
In the linear region, L < 1, with L=bT
we find the universal constant, b,
to have a value around b = 0.070 +/- 0.007.
This small value of b leads to
the crossover region corresponding to large values of T of around
102 to 106.
Expressed in terms of Reynolds numbers, Re = L dL/dT,
the crossover region does not appear so
broad, occuring in the range 1 < Re < 100.
In the inertial region, T > 106,
with L=cT2/3 the universal constant c
is around c = 1.
We don't see any evidence for the
prediction[Grant and Elder(1999)]
of a further reduction in scaling
exponent to a regime of domain size scaling as T1/2,
but this does not rule it out further into the inertial regime
than we were able to simulate.
(Return to top.)
References
- Kendon et al.(1999)
-
V M Kendon, J-C Desplat, P Bladon, and M E Cates.
3-D spinodal decomposition in the inertial regime.
cond-mat/9902346, 1999.
- Bray(1994)
-
A J Bray.
Theory of phase-ordering kinetics.
Adv. Phys., 43:-459, 1994.
- Grant and Elder.
-
M Grant and K R Elder.
Spinodal decomposition in fluids.
Phys. Rev. Lett., 81:-14, 1999.
- Swift et al.(1996)
-
M R Swift, E Orlandini, W R Osborn, and J Yeomans.
Lattice Boltzmann simulations of liquid-gas and binary fluid systems.
Phys. Rev. E, 54:-5052, 1996.
- Bladon and Desplat.
-
P Bladon and J-C Desplat.
Ludwig: A general purpose Lattice-Boltzmann code.
in preparation.
Revision: 18th April 1999
(Return to top.)
 ed.ac.uk
ed.ac.uk